Os conjuntos numéricos foram criados para agrupar números que possuem características semelhantes
Photo by Mika Baumeister on Unsplash
Números Naturais
O primeiro conjunto numérico que iremos tratar são os Números Naturais. Estes são representados pela letra N .
Assim N = {0,1,2,3,4,5…}. Quando encontramos N com um asterisco, estamos falando de um subconjunto que envolve todos os números naturais não nulos, ou seja, todos com
exceção do zero, N* = {1,2,3,4,5…}.
Matemáticos sempre estão discutindo se o conjunto dos naturais possui zero ou não, então na dúvida é sempre interessante usar o asterisco para dizer que você está dizendo, com certeza, este conjunto aqui só tem números positivos!
Números Inteiros
Outro conjunto são os Números Inteiros, eles surgem no Renascimento, quando os matemáticos precisavam de novos tipos de números que pudessem ser solução de equações lineares como x + 2 = 0, mas a noção de números negativos já existia em outros lugares do mundo antes disso. Eles são
representados pela letra Z (do alemão Zahlen = números).
Z = {…,-2, -1, 0, 1, 2, …). Percebe-se que todo número natural é inteiro, assim N ⊂ Z (N é um subconjunto de Z, pois não há nenhum número em N que não esteja em Z). Este conjunto também possui alguns outros subconjuntos notáveis.
Z* = inteiros não nulos (sem o zero)
Z+ = inteiros não negativos (maiores ou iguais a zero)
Z*+ = inteiros positivos (tira o zero)
Z– = inteiros não positivos (menores ou iguais a zero)
Z*– = inteiros negativos (tira o zero)
Os números inteiros são fechados em relação às operações de adição, subtração e multiplicação, ou seja, sempre que realizarmos uma dessas operações como números inteiros, o resultado será um número inteiro. Os naturais também são fechados para soma e multiplicação.
Números Racionais
Números Racionais, representado por Q
São números que podem ser expressos na forma A/B, onde A e B são inteiros, com B diferente de zero (não nulo), Assim Q = {a/b com a ∈ Z e b ∈ Z*}, por exemplo 5; 0,3333…; (?)…. Todo número inteiro é racional, sendo assim, Z é um subconjunto de Q. Todo e qualquer número racional pode ser
exemplificado por uma dízima exata ou por uma dízima periódica (infinita).
Eles podem ser representados em fração, número misto, número decimais, fração geratriz e dízimas periódicas.
Entretanto, nem todo número pode ser escrito como a razão entre dois números inteiros, como a √2 (raíz quadrada de 2).
Números Irracionais,
Para representar estes, foi criado um outro conjunto, os Números Irracionais, representados pela letra I.
Os números irracionais são aqueles em que as dízimas são infinitas, porém não periódicas. Eles não podem ser expressos na forma de a/b com a e b inteiros e b diferente de zero.
Os números irracionais (I) são raízes não racionais (de números que não são potências), Logaritmos em que o logaritmando não é uma potência de expoente racional da base e algumas constantes que
denotamos por símbolos especiais (φ, π, e…. embora pi e o número de Euler tenham particularidades até hoje não muito bem compreendidas).
Números Racionais
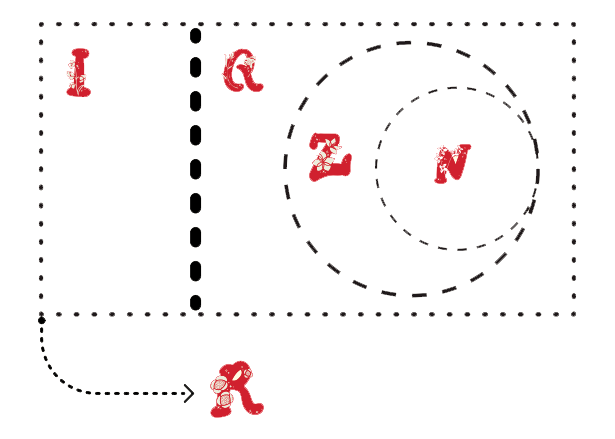
A reunião dos Números Racionais (que engloba Z e por consequência N) e dos Números Irracionais (I) forma os Números Reais, representados por R.
É importante ressaltar duas coisas: se um número é racional ele não é irracional, se é irracional não é racional, Q e I são disjuntos (não possuem nenhum número em comum e, portanto, nenhuma intersecção); e todo número real é racional ou irracional, não existe número real fora desses dois.
Os números reais podem ser representados geometricamente por uma reta, onde cada ponto corresponde a um número real e cada número real corresponde a um ponto da reta (não sobram
pontos nem números sem um equivalente).

Subpartes contínuas da reta são chamadas intervalos, e são, na verdade, subconjuntos de R determinados por desigualdades.
- Intervalo aberto: [a,b] ou (a,b) = {x e R | a < x < b} - o intervalo vai de a até b, mas a e b não entram no intervalo.
- Intervalo fechado: [a,b] = {x e R | a ≤ x ≤ b} – o intervalo vai de a até b.
- Intervalo fechado à esquerda e aberto a direita: [a,b[ ou [a,b) = {x e R | a ≤ x < b} - o intervalo vai a até b, mas b não entra no intervalo.
- Intervalo aberto à esquerda e fechado a direita: ]a,b] ou (a,b]
= {x e R | a < x ≤ b} - o intervalo vai de a até b, mas a não entra no intervalo
Geometricamente na reta podemos marcar os intervalos reforçando a sublinha e com bolinhas nos seus limites. Se o limite está incluso no intervalo, colocamos um círculo preenchido, se não, estará como um O — com o interior vazio.
Esse material é uma parceria entre Cliquevestibular e Organizo, Logo Passo 2021
PRODUÇÃO
ISABELA XAVIER
AKIRA DEMENECH
ANA MARIANE